Heaps are the most efficient data structure when it comes to accessing the smallest or largest element in constant time (O(1)). Python provides the heapq module (heap queue or priority queue) which simulates min heap using lists. This tutorial walks you through how to use heaps in Python with practical examples.
What is a Heap?
A heap has multiple meanings in computer science. Sometimes, it refers to a memory area in a program used for dynamic allocation. However, in this tutorial, we are talking about the Heap Data Structure, which is a complete binary tree. It helps in implementing priority queues (PQ), the heapsort, and some graph-based algorithms.
A heap has the following two variants:
- A max-heap, in which the parent is more than or equal to both of its child nodes.
- A min-heap, in which the parent is smaller or equal to the child nodes.
Below is a general representation of a min heap.
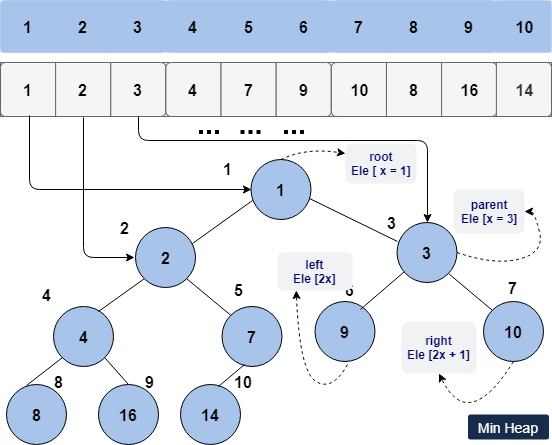
Also Read: Python Array Explained with Examples
The Benefits of a Heap
A heap provide the following benefits:
- Fast Access to Min/Max: It keeps the root element always the smallest (min-heap) or largest (max-heap) element. This is ideal for priority queues where you frequently need the “highest priority” item.
- Efficient Insertions and Deletions: It ensures that adding or removing the root element takes only O(log n) time — much faster than using a naive list, where finding the min/max takes O(n) time.
- Flexible usage: Heaps are used in algorithms like Dijkstra’s (shortest path), Heap Sort, and scheduling tasks by priority.
Using Python heapq Module
Python’s heapq module provides a min-heap implementation using a binary heap structure. It offers seven key functions to work with priority queues, split into two categories:
Four of them are primarily used for basic heap operations: heappush, heappop, heapify, and heapreplace. These functions require you to pass a list explicitly, as the heap is maintained directly on the list itself.
The remaining three functions—nlargest, nsmallest, and merge—are utility functions that work with iterables and provide advanced functionality such as finding the top N elements or merging multiple sorted inputs efficiently.
The heap data structure has a property that it always pops out the smallest of its elements (Min Heap). Also, it keeps the heap structure intact despite any push or pop operation. The heap[0] would also point to the smallest value of the Heap.
Let’s now check out what functions this module provides.
Python heapq Functions
The heapq module has the following methods:
heappush()
It adds an element to the heap. Don’t apply it on any old list, instead use the one that you built using Heap functions. That is how you can ensure the elements are in the desired order.
# heappush() Syntax
import heapq as hq
hq.heappush(heap, element)Check out the below heapq’s heappush() function example.
# A brief heapq.heappush() example
import heapq as hq
import random as r
init_list = list(range(10, 99, 10))
print("Step-1: Seed data for the heap: ", init_list)
r.shuffle(init_list)
print("Step-2: Randomize the seed data: ", init_list)
# Creating heap from an empty list
heap = []
print("Step-3: Creating heap...")
# Demonstrating heapq.heappush() function
[hq.heappush(heap, x) for x in init_list]
# Printing heap content to see if the smallest item is at 0th index
print(" a. Heap contains: ", heap)
# Adding another smaller item to the heap
hq.heappush(heap, 1)
print(" b. Heap contains: ", heap)This code results in the following:
Step-1: Seed data for the heap: [10, 20, 30, 40, 50, 60, 70, 80, 90]
Step-2: Randomize the seed data: [70, 20, 60, 80, 90, 30, 40, 10, 50]
Step-3: Creating heap...
a. Heap contains: [10, 20, 30, 50, 90, 60, 40, 80, 70]
b. Heap contains: [1, 10, 30, 50, 20, 60, 40, 80, 70, 90]You can observe that the heap kept the smallest item at the 0th index. We added a new lower value using the heappush() function. And, it pushed that to the 0th position by shifting the previous value to the 1st index.
heappop()
It is used to remove the smallest item that stays at index 0. Moreover, it also ensures that the next lowest replaces this position:
# heappop() Syntax
import heapq as hq
hq.heappop(heap)Check out the heapq’s heappop() example. You need to append this code to the previous heappush() example.
# Exercising heapq.heappop() function
print("Step-4: Removing items from heap...")
out = hq.heappop(heap)
print(" a. heappop() removed {} from heap{}".format(out, heap))
out = hq.heappop(heap)
print(" b. heappop() removed {} from heap{}".format(out, heap))
out = hq.heappop(heap)
print(" c. heappop() removed {} from heap{}".format(out, heap))It will give the following result:
Step-4: Removing items from heap...
a. heappop() removed 1 from heap[10, 20, 40, 50, 30, 70, 80, 90, 60]
b. heappop() removed 10 from heap[20, 30, 40, 50, 60, 70, 80, 90]
c. heappop() removed 20 from heap[30, 50, 40, 90, 60, 70, 80]It is clear from the output that heappop() always pops off the lowest element from the heap.
heappushpop()
This function first adds the given item to a Heap, then removes the smallest one and returns it. So, it is an increment of both heappush() and heappop(). But it tends to be a little faster than the two combined.
# heappushpop() Syntax
import heapq as hq
hq.heappushpop(heap, element)Check out the heapq’s heappushpop() example. You need to append it to the previous code sample.
# Exercising heapq.heappushpop() function
print("Step-5: Adding & removing items from heap...")
new_item = 99
out = hq.heappushpop(heap, new_item)
print(" a. heappushpop() added {} and removed {} from heap{}".format(new_item, out, heap))
new_item = 999
out = hq.heappushpop(heap, new_item)
print(" b. heappushpop() added {} and removed {} from heap{}".format(new_item, out, heap))The output is:
Step-5: Adding & removing items from heap...
a. heappushpop() added 99 and removed 30 from heap[40, 60, 50, 70, 90, 99, 80]
b. heappushpop() added 999 and removed 40 from heap[50, 60, 80, 70, 90, 99, 999]heapify()
This function accepts an arbitrary list and converts it to a heap.
# heapify() Syntax
import heapq as hq
hq.heapify(heap)Here is how we can use the heapify()function.
# A brief heapq.heapify() example
import heapq as hq
heap = [78, 34, 78, 11, 45, 13, 99]
print("Raw heap: ", heap)
hq.heapify(heap)
print("heapify(heap): ", heap)After running the above code, we get the following result:
Raw heap: [78, 34, 78, 11, 45, 13, 99]
heapify(heap): [11, 34, 13, 78, 45, 78, 99]You can see that the heapify() function transformed the input list and made it a heap.
heapreplace()
It deletes the smallest element from the Heap and then inserts a new item. This function is more efficient than calling heappop() and heappush().
# heapreplace() Syntax
import heapq as hq
hq.heapreplace(heap, element)Have a look at the below heapq’s heapreplace() function example.
# A brief heapq.heapreplace() example
import heapq as hq
heap = [78, 34, 78, 11, 45, 13, 99]
hq.heapify(heap)
print("heap: ", heap)
hq.heapreplace(heap, 12)
print("heapreplace(heap, 12): ", heap)
hq.heapreplace(heap, 100)
print("heapreplace(heap, 100): ", heap)The output is:
heap: [11, 34, 13, 78, 45, 78, 99]
heapreplace(heap, 12): [12, 34, 13, 78, 45, 78, 99]
heapreplace(heap, 100): [13, 34, 78, 78, 45, 100, 99]nlargest()
This function returns the n largest elements from a given iterable. It also accepts a key which is a function of one argument.
The selected items have to satisfy the k function. If any of them fails, then the next higher number is considered.
# nlargest() Syntax
import heapq as hq
hq.nlargest(n, iterable, key=None)Let’s see how the heapq’s nlargest() function works. We called it to get the two largest numbers.
# heapq.nlargest() example without a key
import heapq as hq
heap = [78, 34, 78, 11, 45, 13, 99]
hq.heapify(heap)
print("heap: ", heap)
out = hq.nlargest(2, heap)
print("nlargest(heap, 2): ", out)The result is:
heap: [11, 34, 13, 78, 45, 78, 99]
nlargest(heap, 2): [99, 78]Check out another heapq’s nlargest() function example. It not only requests for the two largest numbers but also has a is_even() function as the KEY.
If any of the selected numbers fail to clear the KEY function, then the next one comes in.
# heapq.nlargest() example with key
import heapq as hq
def is_even(num):
if num%2 == 0: return 1
return 0
heap = [78, 34, 78, 11, 45, 13, 99]
hq.heapify(heap)
print("heap: ", heap)
out = hq.nlargest(2, heap, is_even)
print("nlargest(heap, 2): ", out)The output is:
heap: [11, 34, 13, 78, 45, 78, 99]
nlargest(heap, 2): [34, 78]nsmallest()
It is also similar to the nlargest() in operation. However, it gets the n smallest elements from a given iterable. It too accepts a key which is a function of one argument.
The selected items have to satisfy the k function. If any of them fails, then the next smaller number is considered.
# nsmallest() Syntax
import heapq as hq
hq.nsmallest(n, iterable, key=None)Here is a simple example of using the heapq nsmallest() function. We called it to fetch the two smallest numbers.
# heapq.nsmallest() example
import heapq as hq
heap = [78, 34, 78, 11, 45, 13, 99]
hq.heapify(heap)
print("heap: ", heap)
out = hq.nsmallest(2, heap)
print("nsmallest(heap, 2): ", out)Here is the result:
heap: [11, 34, 13, 78, 45, 78, 99]
nsmallest(heap, 2): [11, 13]You can achieve similar behaviour in other ways, but the heap algorithm is more memory-efficient and even faster.
Let’s now solve a basic problem to see how a min-heap works in practice.
Python heapq Example
You may eventually solve many programming problems using its functions. For example, find the two largest numbers from a list of integers in Python.
There happen to be many ways to address this problem. However, none is as intuitive and faster than a Heapq solution.
Out of many Python heapq functions, one is nlargest(). It returns a list-type object containing the desired number of largest elements. Below is a short example before we dig into the more complicated ones.
# A brief heapq example
# Find the two largest integers from a list of numbers
import heapq as hq
list_of_integers = [21, 67, 33, 13, 40, 89, 71, 19]
# Find two largest values
largest_nums = hq.nlargest(2, list_of_integers)
print("Two largest numbers are: ", largest_nums)The output is:
Two largest numbers are: [89, 71]Please note that you can create a heap in either of these two ways:
- Initialize the list with [].
- Pass a pre-filled list into
heapify()to convert to a heap.
Python heapq Exercises
Now, have some exercises where you can practically use the heapq.
Add and Remove Elements from a Heap
Write a Python program to push elements and pop off the smallest one.
import heapq as hq
heap = []
hq.heappush(heap, ('H', 9))
hq.heappush(heap, ('H', 7))
hq.heappush(heap, ('H', 4))
hq.heappush(heap, ('H', 1))
print("Elements in the heap:")
for ele in heap:
print(ele)
print("----------------------")
print("Calling heappushpop() to push element on the heap and return the smallest one.")
hq.heappushpop(heap, ('H', 11))
for ele in heap:
print(ele)The output:
Elements in the heap:
('H', 1)
('H', 4)
('H', 7)
('H', 9)
----------------------
Calling heappushpop() to push element on the heap and return the smallest one.
('H', 4)
('H', 9)
('H', 7)
('H', 11)Implement Heap Sort Using heapq Module
Write a Python program to perform Heap Sort, push all items to a heap, and then take off the smallest ones one after the other.
import heapq as hq
def heap_sort(heap):
in_list = []
for value in heap:
hq.heappush(in_list, value)
return [hq.heappop(in_list) for i in range(len(in_list))]
out = heap_sort([9, 7, 5, 2, 1, 2, 8, 10, 6, 5, 4])
print(out)Here is the result:
[1, 2, 2, 4, 5, 5, 6, 7, 8, 9, 10]Python heapq Module: Key Questions Answered
There are many other problems that you may like to solve. Some of these are as follows:
Where is the third smallest key in a heapq min-heap?
The third smallest key isn’t directly accessible. You must call heappop() three times (1st pop = smallest, 2nd pop = 2nd smallest, 3rd pop = 3rd smallest).
Where is the largest key in a heapq min-heap?
The largest key is always in one of the leaf nodes, but its exact position isn’t fixed. Use heapq.nlargest(1, heap) to find it efficiently.
When do heapq insertions take Ω(n log n) time?
When inserting n elements one-by-one into an empty heap. Each heappush takes O(log n) time, resulting in n × O(log n) = Ω(n log n) total time.
Must Read: How to Create Linked Lists in Python
Final Thoughts: Mastering Python’s heapq Module
The heapq module provides an efficient way to implement priority queues, schedulers, and sorting algorithms—essential tools for:
- AI & Machine Learning (e.g., priority task scheduling)
- Operating Systems (e.g., process scheduling)
- Graph Algorithms (e.g., Dijkstra’s shortest path)
Next Steps:
- Practice with real-world examples (e.g., merge k-sorted lists, top-k elements).
- Deepen your Python skills with our beginner-to-advanced Python tutorial.
Enjoyed this guide? Help others discover it by sharing on Twitter or LinkedIn. Your support keeps our content free!
Keep Learning!





